Calorimetria-Exercícios Resolvidos-3

LISTA 2: calorimetria / equilíbrio térmico  - ETEc GV (Automação 3º Ano, 2017)

Dados:

Exercício-01

Tem-se 0,10 Kg de vapor de água a 120 ºC, a pressão atmosférica normal constante, que deve ser transformado em gelo a – 10 ºC.

a) Determine a quantidade de calor necessária para transformar esse vapor em gelo a – 10 ºC.

b) Construa o gráfico de Temperatura x Quantidade de Calor Cedido nessa transformação.

Solução:

Fazendo um croqui do processo para melhorar a visualização.

As quantidades de calor que vamos calcular são calores cedidos (=perdidos).

Portanto, a quantidade de calor total cedido no processo é Q = 311,1 KJ.

O gráfico de Temperatura x Quantidade de Calor Cedido.  Colocando os valores de temperatura no eixo das abscissas, tem-se:

Exercício-02

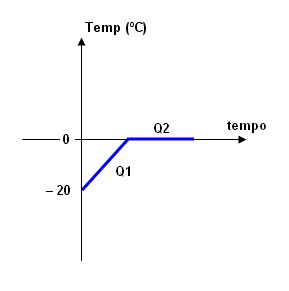
Uma pedra de gelo de 100 g a – 20 ºC é colocada num recipiente com 300 g de água a 60 ºC.  Admitindo-se que o sistema esteja à pressão atmosférica normal e desprezando o calor cedido pelo recipiente, determine a temperatura de equilíbrio térmico.

Solução:

Supondo que todo o gelo derreteu e a temperatura de equilíbrio seja superior a 273 K (0 ºC).  Vejamos a figura:

Em equilíbrio térmico:

Q₁ + Q₂ + Q₃ + Q₄ = 0

0,3_*4,2x10³_*(θ_e ‒ 333) + 0,1_*4,2x10³_*( θ_e ‒ 273) + 0,1_*3,3x10⁵ + 0,1_*2,1x10³ _*(273 – 253) = 0

1260.(θ_e ‒ 333) + 420.(θ_e ‒ 273) + 33000 + 4200 = 0

1680.θ_e ‒ 534240 + 37200 = 0  → 1680.θ_e = 497040  → θe = 295,857 K → θe = 22,86 ºC

A suposição inicial está correta.

Outra maneira de resolver:

Supondo que nem todo gelo derreteu.

Gelo:

Q = m*c*Δθ = 100*0,5*20 = 1000

Q = m.L = 100*80 = 8000

ΣQ = 1000 + 8000 = 9000 cal (Qg)

Água:  (60º → 0ºC)

Q = m*c*Δθ = 300*1*60 = 18 000 cal  (Qa)

Qa > Qg  ↔ 18000 cal > 9000 cal

Portanto, derrete todo o gelo, logo sobram 18 000 – 9 000 = 9 000 cal

Água derretido + água

Q = m*c*Δθ  → 9000 = (300 + 100)*1* Δθ → Δθ = 22,5ºC

Portanto, a temperatura final do sistema é: 22,5ºC

Logo, o gráfico correto é:

Exercício-03

Para se determinar o calor específico de que é feito um corpo de massa 500 g, inicialmente a 70 ºC ele é colocado junto com 400 g de água a 20 ºC. O equilíbrio se estabelece aos 30 ºC. Nestas condições calcule o calor específico de que é feito o corpo em cal/g.ºC. (dado 1 cal = 4,18 J)

Solução:

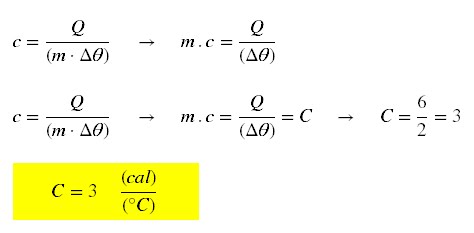
Em equilíbrio térmico: Q₁ + Q₂ = 0

0,500.c.(303 – 343) + 0,400.4,2.10³.(303 – 293) = 0

-20c + 16800 = 0 → c = 840 J/Kg.K  → c = 840/(1000.4,18.1) = 0,2

c = 0,2 cal/g.ºC

Exercício-04 (FATEC – SP)

Uma xícara com 200 g de água quente é esfriada tendo a temperatura diminuída de 20 ºC.  Considere o calor específico da água igual a 1,0 cal/g.ºC e o calor de fusão do gelo igual a 80 cal/g.  A quantidade de calor perdida por essa água é suficiente para fundir quantas gramas de gelo fundente?

Solução:

xícara: m = 200 g, Δθ = 20 ºC (= diferença de temperatura), 1,0 cal/g.ºC

No processo de resfriamento a água libera a quantidade de calor igual a:

Q = m.c. Δθ = 200.1.20 = 4000 cal

Gelo fundente: m = ?, L = 80 cal/g

Essa energia provoca a fusão de m gramas de gelo fundente:

Q = m.L ↔ 4000 = m.80 ↔ m = 50 g

Exercício-05

Um fragmento de alumínio de 10 g à temperatura de 80 ºC é colocada em 10 g de água à temperatura de 20 ºC.  Sendo o calor específico do alumínio 0,2 cal/g.ºC e o calor específico da água é 1 cal/g.ºC, determine a temperatura de equilíbrio térmico.

Solução:

Alumínio:

m = 10 g; θi = 80ºC; c = 0,2 cal/gºC

Água:

m = 10 g;  θi = 20ºC; c = 1 cal/gºC

Desenhando a figura do processo:

No equilíbrio tem-se: Q_Al + Q_H20 = 0

m_Al*c_Al*(θe – 80) + m_H2O*c_H2O*(θe – 20) = 0

10_*0,2_*( θe – 80) + 10_*1_*(θe – 20) = 0

2_*( θe – 80) + 10_*(θe – 20) = 12_*θe – 360 = 0 → 12_*θe = 360 → θe = 30 ºC

Exercício-06

Numa bacia que contém 18 litros de água à temperatura de 24 ºC pode-se obter uma mistura à temperatura final de 36 ºC.  Desprezando-se a capacidade térmica da bacia e as perdas para o ambiente, quanto de água a 72 ºC deverá ser acrescentado na bacia?

Solução:

Fazendo o gráfico de acordo com o enunciado:

Sabemos que : 18 litros = 18 Kg = 18 000 g

Q₁+ Q₂ = 0

18000.1.(36 – 24) + m.1.(36 – 72) = 0 ↔ 216000 – 36.m = 0 → m = 6000 g

m = 6000 g = 6 Kg ↔ V= 6 litros

Exercício-07 (FUVEST)

Um ser adulto e saudável consome, em média, uma potência de 120 J/s.  Uma “caloria alimentar” (1 kcal) corresponde, aproximadamente, a 4,0x10³ J.   Para mantermos saudáveis, quantas “calorias alimentares” devemos utilizar, por dia, a partir dos alimentos que ingerimos?

Solução:

P = 120 J/s  ↔ P = Q/t

Quanta energia consumirá por dia se um humano consome 120 J em 1 segundo?

1 dia = 24x60x60 = 86400 s.

Por regra de três, temos:

120 J  ---------- 1 s

   x     ----------  86400 s

x = 120 x 86400 = 10368000 J

Convertendo para kcal:

1 kcal ----------- 4,0 x 10³ J

   y     ------------ 10368000 J

y = 10368000/4000 = 2592 → y = 2592 Kcal

Exercício-08 (Mackenzie)

Uma fonte calorífica fornece calor continuamente, à razão de 150 cal/s, a uma determinada massa de água. Se a temperatura da água aumenta de 20 ºC para 60 ºC em 4 minutos, sendo o calor específico sensível da água 1,0 cal/g.ºC, qual é a massa de água aquecida, em gramas?

Solução:

Fazendo o gráfico de acordo com o enunciado:

Quantidade de calor necessário para aumentar a temperatura de 20ºC para 60ºC é:

150 cal ------ 1 s

x -------------- 240 s

x = 36 000 cal

Seja m a massa de água, então temos:

Q = m.c.Δθ → 36000 = m.1.(60 – 20) = 40.m → m = 900 g

Exercício-09 (PUCCAMP)

Uma barra de cobre de massa 200 g é retirada do interior de um forno, onde estava em equilíbrio térmico, e colocada dentro de um recipiente de capacidade térmica 46 cal/ºC que contém 200 g de água a 20 ºC.  A temperatura final de equilíbrio é de 25 ºC.  Calcule a temperatura do forno, em ºC.   Dado: c_CU = 0,03 cal/g.ºC

Solução:

Pelo princípio da calorimetria (conservação de energia)
(Q1 – barra de cobre; Q2 – recipiente; Q3 – água)

Q1 + Q2 + Q3 = 0


Fazendo um croqui para visualizar melhor o processo de troca de calor:

Calorimetria-Exercícios Resolvidos-4

Exercício-01

O diagrama representa a quantidade de calor absorvida por dois corpos A e B de massas iguais em função da temperatura.  A relação entre os calores específicos dos corpos A e B é:

a) 2/3            b) 3/4             c) 4/9              d) 9/4

Solução:

Resp. Alternativa: d

Exercício-02

No exercício anterior, a capacidade térmica do corpo A vale:

a) 6 cal/ºC         b) 3 cal/ºC          c) 2 cal/ºC        d) 4/3 cal/ºC

Solução:

Resp. Alternativa: b

Exercício-03

Ainda considerando o exercício-01, se a massa do corpo B é 12 gramas, o calor específico da substância que o constitui vale:

a) 0,5 cal/g.ºC       b) 16 cal/g.ºC        c) 1/9 cal/g.ºC       d) 4/3 cal/g.ºC  

Solução:

Resp. Alternativa: c

Exercício-04

Sabe-se que o calor latente de fusão do gelo é 80 cal/g, o calor específico do gelo é 0,5 cal/g.ºC e o calor específico da água é 1 cal/g.ºC.  A quantidade de calor necessária para fundir um bloco de gelo de massa 500 g inicialmente à temperatura de – 20ºC é:

a) 40000 cal      b) 45000 cal      c) 35000 cal      d) 5000 cal     e) n.d.a

Solução:

m = 500 g

Δθ = 20 ºC

c = 0,5 cal/g.ºC

L = 80 cal/g

Q1 = m.c. Δθ = 500*0,5*20 = 5000 cal

Q2 = m_*L= 500*80 = 40000 cal

Portanto, calor necessário para fundir todo o gelo é:

Q = Q1 + Q2 = 5000 + 40000 = 45000 → Q = 45 000 cal

Resp. Alternativa: b

Exercício-05

São dados calor específico do gelo igual a 0,5 cal/g.ºC;  calor específico da água igual a 1 cal/g.ºC; calor latente de fusão do gelo igual a 80 cal/g.  A quantidade de calor necessária para aquecer 90 gramas de gelo de –10 ºC a + 10 ºC é de:

a) 9000 cal       b) 7500 cal      c) 5550 cal      d) 12 450 cal       e) 8550 cal

Solução:

A quantidade total de calor necessária é:

Q = Q1 + Q2 + Q3

Q1 = m*c*(θf – θi) = 90*0,5*(0 – (‒10)) = 450 cal

Q2 = m*L = 90*80 = 7200 cal

Q3 = m*c*(θf – θi) = 90*1*(10 – 0) = 900 cal

Portanto, Q = 450 + 7200 + 900 = 8550  → Q = 8550 cal

Resp. Alternativa: e

Exercício-06

Queremos determinar o calor latente de vaporização da água. Para tal, dispomos de uma massa de água a 20ºC e de uma fonte de calor de potência constante. Verificou-se que a massa de água em contato com a fonte de calor atinge o ponto de ebulição depois de 20 segundos.  Continuando em contato com essa fonte, toda massa foi vaporizada, após o início da ebulição, em 130 segundos.  Qual o calor latente de vaporização da água?

a) 32,5 cal/g       b) 325 cal/g      c) 52 cal/g      d) 520 cal/g       e) n.d.a

Solução:

Q = m*c*Δt = m*1*(100 – 20) = 80*m → Q = 80*m

Houve vaporização total em 130 s.

Fonte de calor de potência constante, portanto;

Q absorvida em 20 s  →  80*m ------ 20 s

                                          Q’ ← ----- 130 s

Q’ = 520*m

Q’ = m*L

m*L = 520*m → L = 520 cal/g

Resp.Alternativa: d

Exercício-07

Uma esfera de chumbo de massa igual a 2 Kg é aquecida até 100ºC e, em seguida, colocada num calorímetro contendo 2 Kg de água a 25ºC.  Após atingido o equilíbrio térmico, observou-se um aumento de 25/3 ºC na temperatura da água.  Qual o calor específico do chumbo?  Dado calor específico da água = 1 cal/g.ºC.

a) 1 cal/g.ºC     b) 1/8 cal/g.ºC     c) 1/4 cal/g.ºC        d)  1/6 cal/g.ºC        e) n.d.a.

Solução:

Água:

Δt = t _i – t _f = t _f – 25 ↔ 25/3 = t _f – 25  ↔ t _f = 25 + 25/3 = 100/3  ↔ t _f = 100/3

Chumbo:

Δt = t _i – t _f = 100 – 100/3 =  - 200/3

Q(água) + Q(chumbo) = 2000*1*25/3 + 2000*c*(-200/3) = 0

2000*c*(200/3) = 2000*1*25/3  → c = 1/8 = 0,125 cal/g.ºC

Resp. Alternativa: b

Exercício-08

Massas iguais de água quente e gelo fundente são colocadas num recipiente de capacidade térmica desprezível, resultando no equilíbrio térmico apenas água a 0ºC.  Sendo 80 cal/g o calor latente de fusão do gelo, a temperatura da água quente colocada será:

a) 80 ºC

b) proporcional à massa de gelo e água

c) 0ºC, porque 0ºC em relação ao gelo e água é quente

d) indeterminada, face aos dados

e) n.d.a.

Solução:

Q1 + Q2 = 0

m*80 + m*1*(0 – t _i) = 0 → 80*m = m* t _i  →  t _i = 80 ºC

Resp. Altermativa: a 

Exercício-09

Em um calorímetro são colocados 10 g de gelo, fundente à pressão normal e 10 g de água à temperatura t. Sabendo-se que todo o gelo se funde, que o calor latente de fusão do mesmo à pressão normal é 80 cal/g e que o calor específico da água é 1,0 Kcal/Kg.ºC, certamente:

a) t ≤ 100ºC     b) t < 100ºC     c) t ≥ 80ºC     d) t < 80ºC      e) faltam dados

Solução:

Q1 + Q2 = 0

10*80 + 10*1*(0 – t _i) = 0 → 800 = 10* t _i  →  t _i = 80 ºC

Portanto, t _i ≥ 80 ºC

Resp. Alternativa: c

Exercício-10

Num calorímetro de capacidade calorífica desprezível, colocam-se 150 g de gelo a 0 ºC com 300 g de água a 50 ºC.  Sabendo-se que o calor latente de fusão do gelo é 80 cal/g e que calor específico da água é 1 cal/g.ºC; qual é a temperatura final da mistura, após o equilíbrio térmico?

Solução:

Colocando em gráfico e tabela os dados do enunciado, tem-se:

Supondo que a temperatura final seja maior que zero graus.

Σ(Q) = 0 (mistura em equilíbrio térmico)

Q1 = m.L = 150*80 = 12 000 cal

Q2 = m.c.Δt = 150*1*t _f = (150*t _f) cal

Q3 = m.c.Δt = 300*1*( t _f – 50) = (300*t _f – 15 000) cal

Q1 + Q2 + Q3 = 0

12 000 + (150*t _f) +(300*t _f – 15 000) = 0  → 450*t _f = 3000

t _f = 6,7 ºC

Portanto, a suposição inicial está correta.

Calorimetria-Exercícios Resolvidos-2

Gabarito e Comentários no final

Exercício-01 (ITA)

São dados dois cubos A e B de mesmo material e inicialmente à mesma temperatura T1.  O cubo A tem aresta a e o cubo B, aresta b, tal que a = 2b.  Se ambos os cubos são trazidos à temperatura T2<T1, então, se o cubo B cede ao ambiente uma quantidade de calor Q, o cubo A cederá:

a) 2Q          b) 4Q          c) 8Q          d) Q         e) n.d.a

Exercício-02 (UF-Fluminense)

Três recipientes cilíndricos (1, 2, 3) de massas iguais contendo substâncias líquidas são aquecidos por fontes de calor de mesma potência térmica.  Comparando-se simultaneamente nos três recipientes obtém-se o diagrama anexo; cuja interpretação nos permite afirmar:

a) Se o líquido dos três recipientes for o mesmo, o recipiente 3 contém a maior massa líquida;

b) Se os três recipientes contiverem massas iguais de líquidos diferentes a reta 1 corresponderá ao líquido de maior calor específico;

c) Para um mesmo líquido contido nos três recipientes, as retas deveriam se superpor independendo da massa;

d) A reta 3 é, por certo, relativa ao conjunto (recipiente mais líquido) de maior capacidade térmica;

e) n.d.a.

Exercício-03 (Mack)

Uma amostra de 5 g de um líquido absorve 50 cal por minuto, aquecendo-se desde a temperatura de 15ºC até a temperatura de 308 K, em três minutos.  Nessas condições, o calor específico do líquido é:

a) 0,1 cal/g.ºC    b) 0,1 cal/g.K    c) 1,5 cal/g.K    d) 7,5 cal/g.K    e) 30,0 cal/g.K

Exercício-04 (FESP)

Um corpo recebe calor de uma fonte na razão de 400 cal/min. Sua temperatura sofre uma elevação de 200 ºC em 10 minutos.  A capacidade do corpo é:

a) 400 cal/ºC        b) 200 cal/ºC        c) 40 cal/ºC       d) 20 cal/ºC       e) n.d.a.

Exercício-05 (UE-Londrina)

Um aquecedor elétrico eleva de 10 ºC a temperatura de 1.000 g de água em 10 minutos. Se utilizarmos esse aquecedor durante 10 minutos para aquecermos 1.000 g de óleo, qual será a elevação da temperatura do óleo? (calor específico da água: 1,0 cal/g.ºC; calor específico do óleo: 0,5 cal/g.ºC).

a) 10ºC          b) 20ºC          c) 40ºC          d) 50ºC          e) 100ºC

Exercício-06

100 gramas de certa substância levam 10 minutos para sofrer um aquecimento de 90ºC.   Sendo 0,3 cal/gºC seu calor específico, o fluxo da fonte vale:

a) 250 cal/min        b) 340 cal/min        c) 270 cal/min        d) n.d.a.

Exercício-07 (FM – Santos)

O gráfico da figura representa a quantidade de calor recebida por um corpo em função da temperatura.  Este gráfico, também, faz parte das questões 8 e 9.

A capacidade térmica do corpo em cal/ºC é:

a) 40         b) 480            c) 24           d) 6.000       e) um valor diferente desses

Exercício-08 (FM – Santos)

Se o calor específico for 0,2 cal/gºC, a massa do corpo é de: (utilizar o gráfico da questão 7 e eventualmente, utilizar o resultado da mesma questão.

a) 125        b) 1.000       c) 200         d) 2.000       e) um valor diferente desses

Exercício-09 (FM – Santos)

Se o corpo atingiu o ponto B em 12 minutos, a fonte fornece calor, em cal/min, à razão de:

a) 40        b) 12       c) 480       d) 1.000      e) um valor diferente desses

Exercício-10

Um corpo absorve calor de uma fonte à razão de 1.000 cal/min.  O gráfico da temperatura do corpo em função do tempo está indicado abaixo.  A capacidade calorífica (ou capacidade térmica) do corpo em cal/ºC será:

a) 4,18x107         b) 200         c) 427         d) 500          e) n.d.a.

Gabarito e Comentários

Exercício-1) Alternativa: c

Justificativa:

Cubo B cede ao ambiente uma quantidade de calor Q.

Cubo A 

Exercício-2) Alternativa: b

Justificativa:

A alternativa a está incorreta porque se os líquidos são iguais e fontes de calor têm a mesma potência, o líquido com maior massa esquenta menos então seria recipiente 1 e o recipiente 3 é o que contém menor massa.  É só analisar a fórmula abaixo.

A alternativa b está correta, pois, os recipientes contêm massas iguais e fontes de calor têm a mesma potência, portanto, o líquido com menor calor específico esquenta mais, logo o a reta-1 corresponde ao líquido de maior calor específico.

A alternativa c é incorreta, porque líquidos iguais, porém, massas diferentes, resultam em retas não coincidentes.

A alternativa d é incorreta, porque quanto maior a capacidade térmica, menor será a temperatura, portanto, a reta-3 corresponde ao menor capacidade térmica.

Exercício-3) Alternativa:c

Justificativa:

m = 5 g

Ti = 15 ºC = 288 K

Tf = 308 K

50 cal ------- 1 min

Q ------------- 3 min

Q = 150 cal

Portanto,

Q = m.c.(Tf-Ti) → 150 = 5*c*(308 – 288) → c = 1,5 cal/g.K

Exercício-4) Alternativa: d

Justificativa:

400 cal ------------ 1 min

Q -----------------  10 min

Q = 4000 cal

Δθ = 200 ºC

Q = m*c*Δθ = C*Δθ → C = Q/Δθ = 4000/200 = 20 → Q = 20 cal/ºC

Exercício-5) Alternativa: b

Justificativa:

Quantidade de calor para aquecer água de 10 ºC em 10 min foi de:

m_água = 1000 g

c_água = 1 cal/gºC

Q_água = m_água.c.Δθ_a = 1000_*1_*10 = 10000 cal

Calculando a elevação da temperatura do óleo, utilizando a mesma quantidade de calor.

m_óleo = 1000 g

c_óleo = 0,5 cal/gºC

Q = 10000 cal

10000 = 1000*0,5*Δθ_o  → Δθ_o = 20 ºC

Exercício-6) Alternativa: c

Justificativa:

m = 100 g

Δt = 10 min

c = 0,3 cal/g.ºC

Δθ = 90 ºC

Q = m.c.Δθ = 100.0,3.90 = 2700 cal

2700 cal --------- 10 min

X ------------------  1 min

X = 270 cal/min

Exercício-7) Alternativa: a

Justificativa:

De gráfico:

ΔQ = 500 – 20 = 480 cal

Δθ = 12 ºC

ΔQ = m.c.Δθ ↔ ΔQ = C.Δθ ↔ 480 = C.12 ↔ C = 40 cal/ºC

Exercício-8) Alternativa: c

Justificativa:

c = 0,2 cal/g.ºC

m = ?

Q = 480 cal

Δθ = 12 ºC

Q = m.c. Δθ  ↔ 480 = m.0,2.12 ↔ m = 200 g

Exercício-9) Alternativa: a

Justificativa:

Q = 480 cal   --------  12 min

x -----------------------   1 min

x = 480/12 = 40 cal

Portanto, a fonte fornece calor a uma taxa de 40 cal/min.

Exercício-10) Alternativa: d

Justificativa:

Δt = 50 – 30 = 20 ºC

Q = 1000 cal  (em 1 min)

1000 cal ------- 1 min

x ----------------- 10 min

x = 10000 cal

Q = m.c. Δt = C. Δt → C = Q/ Δt = 10000/20 → C = 500 cal/ºC