Ex-01 (ETEc GV – Sistemas Hidráulicos e Pneumáticos - 2016)
Qual a vazão da bomba
hidráulica em litros/minuto para movimentar um êmbolo com Ф 100 mm e velocidade V = 150
mm/s?
Solução:
Como o enunciado pede em
litros por minuto:
Resposta: Q = 70,8 l /min
Ex-02 (ETEc GV – Sistemas Hidráulicos e Pneumáticos - 2016)
Determine a velocidade do
êmbolo do cilindro com Ф 80 mm ,
alimentado por uma bomba cuja vazão é Q = 40 l/min.
Solução
Resposta: V = 132,6 x 10-3 m/s
Ex-03 (ETEc GV – Sistemas Hidráulicos e Pneumáticos - 2016)
Uma bomba hidráulica será
instalada para bombear um volume de óleo de 100 litros em um tempo
de t = 3 min. O desnível entre o fundo
do reservatório e do ponto de descarga é de 1 m . Dados:
ρ(óleo)=8*10² kg/m³; g = 10
m/s²; η(bomba) = 0,8
a)
Qual a potência da bomba em CV?
b)
Calcule o Ф da tubulação sabendo que a bomba trabalha 6h/dia.
c)
Qual a velocidade de deslocamento de óleo na tubulação?
Solução
a) Potência da bomba:
b)
Diâmetro da tubulação (Φ):
Utilizando
a fórmula recomendada pela ABNT (NBR 5626) para cálculo dos diâmetros de
recalque e de sucção para processo intermitente, ou não contínuo.
Onde:
Φ= diâmetro de recalque – em metros (m); T = período - número horas de funcionamento
da bomba por dia e Q = vazão - em metros cúbicos por segundo (m³/s).
c) Velocidade de deslocamento de óleo na
tubulação:
Ex-04
Calcular o tempo que levará
para encher um tambor de 214
litros , sabendo-se que a velocidade de escoamento do
líquido é de 0,3m/s e o diâmetro do tubo conectado ao tambor é igual a 30mm.
Solução
Primeiramente,
cálculo da vazão volumétrica (SI = sistema internacional):
Cálculo do tempo:
Ex-05
Calcular o diâmetro de uma
tubulação, sabendo-se que pela mesma, escoa água a uma velocidade de 6m/s. A
tubulação está conectada a um tanque com volume de 12000 litros e leva 1
hora, 5 minutos e 49 segundos para enchê-lo totalmente.
Solução
1
– Cálculo do tempo em segundos (SI):
1h,
5min e 49s = 3600+300+49=3949 s
Ex-06
Um determinado líquido é
descarregado de um tanque cúbico de 5
m de aresta por um tubo de 5 cm de diâmetro. A vazão no
tubo é 10 l/s, determinar:
a) a velocidade do fluído no
tubo.
b) o tempo que o nível do
líquido levará para descer 20cm.
Solução
a) Cálculo da velocidade do fluido no tubo:
b) Cálculo do tempo que o nível do líquido levará para descer
O
volume correspondente aos 0,20
m de altura do líquido:
V =
5 x 5 x 0,20 = 5 m³
Ex-07
Solução
Pela
lei de Pascal, tem-se: p1 = p2
Ex-08
Um motor ideal é usado para
acionar uma bomba de rendimento igual a 40%, cuja função é elevar 300 litros de água por
minuto a uma altura de 20 m .
Esse motor consome óleo combustível de poder calorífico igual a 4,0 x 107
J/kg. Dados: g = 10 m/s² e ρágua = 1,0 kg/l, responda:
a) Qual é a potência efetiva do motor utilizado nessa
tarefa?
b) Qual foi o consumo de óleo, em kg, utilizado pelo
motor, em uma hora de trabalho?
Solução
Em sistema internacional
(SI).
a) Potência efetiva é igual
à potência útil utilizada para elevação da água:
b) Consumo de óleo em 1 hora de operação:
Potência total:
Energia total em 1 hora:
Usando as informações do
enunciado:
Ex-09
São dados os seguintes
valores:
carga = 1500 N (= F2)
A1 = 5 x 10-4 m²
A2 = 50 x 10-4 m²
H1 = 10 x 10-2 m
g = 10 m/s²
Solução:
Cálculo da força F1
aplicando a Lei de Pascal.

Cálculo do volume necessário
no cilindro-2, para subir 0,2 m .
Cálculo do volume de cada
bombeada:
Portanto, o número de
bombeadas necessárias é:
Ex-10
Solução
Reservatório-1
Reservatório-2
Na seção A
Pela conservação de massa
para um escoamento incompressível (ρ = constante):


















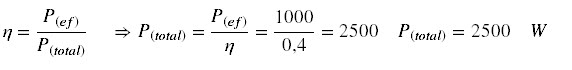










Nenhum comentário:
Postar um comentário