Ex-01
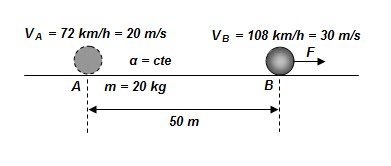
Um ponto material de 20 kg desloca-se numa
trajetória retilínea, sem atrito, sob a ação de uma força F de direção paralela
à trajetória e passa por uma marca A na trajetória, com velocidade vA
= 72 km/h .
Atinge uma marca B distante de A, 50
m , com velocidade vB = 108 km/h e aceleração
escalar constante. Qual o trabalho da força F entre os pontos A e B? Despreze
ações de atrito.
Solução
Pela equação de Torricelli,
vamos calcular a aceleração:
Pela equação fundamental da
dinâmica, vamos calcular a F:
Ex-02
Um móvel sai do repouso pela
ação da força F = 12 N constante, que nele atua durante 4 s, em trajetória
retilínea e horizontal, sem atrito, e o móvel caminha 20 m . Determine: A) a
aceleração adquirida pelo móvel; B) a massa do corpo; C) o trabalho da força F
nos quatro primeiros segundos; D) a velocidade do corpo após 4 s.
Solução
A) Pela equação da
velocidade:
Pela equação de Torricelli:
Substituindo (1) em (2):
B) A massa do corpo:
C) Trabalho da força F:
D) Velocidade após 4
segundos:
Ex-03
Um corpo a 90 km/h vê um obstáculo à sua frente, à distância de 125 m e freia com
retardamento constante. A) Qual o menor valor de retardamento (em m/s²) para
não se chocar com o obstáculo; B) Se a massa do carro é 500 kgf, qual o
trabalho da força de frenagem desde o início da frenagem até o instante final?
Solução
A) Calcular a desaceleração
utilizando a equação de Torricelli:
B) Força de frenagem:
Ex-04 (EPUSP)
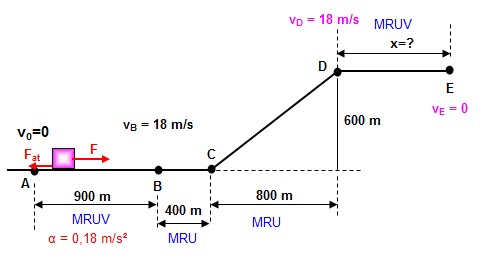
Um corpo de massa m = 500 kg partindo do repouso
em A, percorre a trajetória ABCDE situada num plano vertical. A força F, que atua sobre móvel, mantém-se sempre paralela à velocidade
do corpo e assume valores diferentes em cada trecho da trajetória, de tal forma
que o trecho AB é percorrido com aceleração constante de 0,18 m/s²; os trechos
BC e CD são percorridos com movimento uniforme; a partir do ponto D a força F
se anula. O coeficiente de atrito em toda a trajetória é μ = 0,10. Admita g =
10 m/s². A) Em que trecho a força F é maior que a força de atrito? B) qual a
distância DE = x que o corpo percorre até parar? C) Qual o trabalho da força F
ao longo da trajetória?
Solução
A) No trecho AB a força F é
maior que a força de atrito, pois o corpo se movimenta com aceleração constante
de 0,18 m/s² e no trecho CD porque compensa a componente do peso para que o
movimento seja uniforme.
B) Cálculo da distância x:
Vamos calcular a velocidade
no ponto B, pois, a partir deste ponto a velocidade é constante até o ponto D.
Por Torricelli:
No trecho DE só existe força
de atrito e esta força está contra o movimento, portanto, para calcular a
desaceleração, tem-se:
Novamente, por Torricelli:
C) O trabalho da força F em todo o trecho é
igual ao trabalho no trecho AB + trecho BC + trecho CD:
No trecho AB:
No trecho BC:
No trecho CD:
No trecho DE:
O trabalho da força F é
nulo, pois, a força F neste trecho é zero.
Trabalho total da força:
Ex-05
Um barco a vela tem massa
igual a 200 kg
e está parado num lago de águas tranqüilas. A vela do barco é de forma
triangular com base igual a 2 m
e altura 4 m .
Começa a soprar o vento em direção normal à vela exercendo uma pressão uniforme
de 0,2 N/m², movimentando o barco em linha reta. Após 5 minutos o barco
choca-se com rochedo. Determine a distância d entre o barco e o rochedo, quando
iniciou o movimento do barco e o trabalho da força de pressão do vento nesse
deslocamento. Lembre-se de que pressão é igual a força pela área.
Solução
Pela equação fundamental da
mecânica:
Pela equação horária do
barco:
O trabalho da força do
vento:
Ex-06
Um
corpo move-se numa trajetória retilínea sob a ação de uma força F paralela à
trajetória. Despreze o atrito. O gráfico de sua velocidade em função do tempo é
apresentado na figura. Se a massa do corpo é 0,5 kg: A) em que trecho o
movimento é uniforme? B) em que trecho o movimento é retardado? C) qual a
intensidade da força F em cada trecho do movimento? D) qual trabalho da força F
em cada trecho do movimento?
Solução
A) No trecho 4 a 10 segundos o movimento é
uniforme.
B) No trecho 10 a 16 segundos o movimento é
retardado.
C) A aceleração é a
inclinação da reta em cada trecho, portanto:
No trecho 0 a 4 segundos, a aceleração é
a = 4/4 = 1 m/s², logo a força é: F=m.a então, F=0,5.1=0,5 → F = 0,5 N
No trecho 4 a 10 segundos, a aceleração é
nula, pois, a velocidade é constante (MU), logo, F=0
No trecho 10 a 16 segundos, a aceleração
é a = - 4/6 = - 0,67 m/s², logo a força é: F=m.a, então, F=0,5.(- 0,67)= - 0,33
→ F = - 0,33 N
D) A área sob a curva em
cada trecho é igual ao espaço percorrido, portanto:
No trecho 0 a 4 segundos: ∆s = 1/2.4.4 = 8 m , logo o trabalho W = F.∆s =
0,5.8 = 4 joule
No trecho 4 a 10 segundos o trabalho da
força é nulo, porque a força é nula.
No trecho 10 a 16 segundos: ∆s = 1/2.6.4
= 12 m ,
logo o trabalho W = - F.∆s = - 0,33.12 = - 3,96 joule
Ex-07
Um carro de massa 500 kg move-se sem
resistências dissipadoras em trajetória retilínea O gráfico da força motora, na
própria direção do movimento, é representado na figura. Determine: A) no
percurso de 0 a
600 m o
trabalho da força motora; B) aceleração do carro quando passa pelo ponto a 400 m da origem.
Solução
A) O trabalho da força
motora no percurso de 0 a
600 m é
igual à área sob o gráfico:
A área do trapézio é igual
ao trabalho.
B) A aceleração do carro,
quando passa pelo ponto 400 m
da origem:
A força é constante entre os
trechos 100 a
500 metros
da origem e tem o valor de 800 N.
Portanto, a força resultante neste trecho é 800 N. Logo:
Ex-08
A figura abaixo mostra um
conjunto de polias usado para facilitar o levantamento de
um peso P. Suponha que o
atrito seja desprezível e que as duas polias de baixo, às
quais está presa a carga,
pesem juntas 20 N . Uma carga de 840N deve ser levantada 12 m .
a) Qual a força mínima F
necessária para levantar a carga?
b) Qual o trabalho executado
para levantar a carga até a altura de H = 12m ?
c) Qual o deslocamento da
extremidade livre da corda?
d) Qual o trabalho executado
pela força F para realizar esta tarefa?
Solução
a) Calculando
a força mínima F necessária para levantar a carga.
Ao puxar a corda
exercendo a força F, executaremos um certo trabalho W. Ao elevar o peso P , o
conjunto de roldanas executará, também, um certo trabalho. Esses dois trabalhos
serão iguais, pois a energia em questão é aquela que fornecemos ao atuar com a força
F. A força mínima que o conjunto de roldanas deve fazer atuar sobre o corpo
para elevá-lo com velocidade constante de uma altura H é igual ao peso do
corpo, logo:
W = P.H
Para elevar o
corpo de uma altura H, deveremos puxar a corda ( com F) de um comprimento L ,
logo:
W = F.L
Como esses trabalhos são iguais, tem-se:
Por analogia com outros
tipos de arranjos de roldanas, descobriremos qual é a relação entre H e L deste
problema.
No arranjo mais simples
(Fig-a), o da esquerda da figura anterior, temos 1 corda e um tirante. No
arranjo seguinte (Fig-b) temos 2 cordas e um tirante e no terceiro arranjo
(Fig-c) temos 3 cordas e um tirante.
No caso do problema temos 4
cordas e um tirante.
Portanto, a força mínima
deve ser de 215 N, para levantar a carga.
b) Calcular o
trabalho executado para levantar a carga até a altura de H = 12m.
c) Calcular o
deslocamento da extremidade livre da corda.
d) Calcular o
trabalho executado pela força F para realizar esta tarefa.
Ex-09
Uma força única age sobre um
corpo que está se movendo em linha reta. A figura a seguir mostra o gráfico da
velocidade em função do tempo para esse corpo. Determine o sinal (positivo ou
negativo) do trabalho realizado pela força sobre o corpo nos intervalos AB ,
BC, CD e DE.
Solução
Trecho AB:
Neste trecho a curva é uma
reta, que passa pela origem, e, portanto, a
velocidade é uma função
crescente do tempo até atingir um certo valor
v1, e tem a forma: v = a1
t
O movimento é unidimensional
e a velocidade é crescente, logo a força atua na direção do deslocamento e
desse modo:
Trecho BC:
Neste trecho a velocidade é
constante v1 , logo a
aceleração é nula e portanto a força resultante também é nula. Consequentemente
o trabalho da força resultante será nulo: W(BC)
= 0
Trecho CD:
Neste trecho a velocidade é
decrescente, iniciando o intervalo com valor v1 e terminando com velocidade nula. A equação é do
tipo: v = v1 + a2*(t
- t2) onde a2
< 0. O movimento é unidimensional e a velocidade é decrescente, logo a
força atua na direção contrária ao deslocamento e desse modo:
Trecho DE:
Neste trecho o corpo começa
a recuar (voltar), com a mesma aceleração a2
do intervalo anterior: v = - a2 ( t - t3 ). O módulo
da velocidade aumenta e ela assume valores negativos cada vez maiores. Ao
contrário do item anterior, o corpo está sendo acelerado e temos força e deslocamento
no mesmo sentido.
Ex-10
Uma arca de 50 kg é empurrada por uma
distância de 6m , com velocidade constante, numa rampa com inclinação de 30º
por uma força horizontal constante. O coeficiente de atrito cinético entre a
arca e a rampa é 0,20. Adotar g = 9,8 m/s².
a) Calcule o trabalho
realizado pela força aplicada.
b) Calcule o trabalho
realizado pelo peso da arca.
c) Calcule o trabalho
realizado pela força de atrito.
Solução
a) Cálculo do trabalho WF
realizado pela força aplicada:
Como a arca se move com
velocidade constante, a aceleração é nula e portanto:
Projetando a força peso nos
eixos x e y, tem-se:
b) Cálculo do trabalho WP realizado
pelo peso da arca.
O peso se opõe ao movimento,
portanto, WP < 0, logo:
c) Cálculo do trabalho
realizado pela força de atrito.
A força de atrito, também,
se opõe ao movimento, portanto, Wa < 0, logo:
Como o movimento
realizado com velocidade constante, implicando que a força resultante do
sistema é nula, logo o trabalho da força resultante é nulo.
Somente lembrando
que o trabalho da Força Normal é nulo porque ela é perpendicular ao movimento
(=deslocamento).
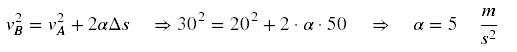


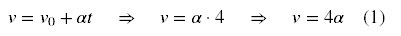

























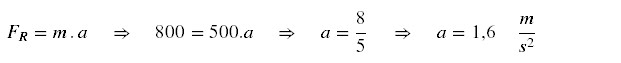









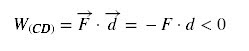
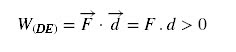







Nenhum comentário:
Postar um comentário