Diferença entre Densidade e Massa específica

Geralmente, usa-se "densidade" para representar a razão entre a massa e o volume de objetos sólidos (ocos ou maciços).  E "massa específica" para fluidos (líquidos e gases) e substâncias.

Um exemplo para ilustrar:

Para ficar mais fácil entender imagine um tambor com uma parte oca dentro, a parte oca está vazia, e o resto do cilindro preenchido de água. 

Supondo que o tambor é ideal, isto é, sua massa e espessura das paredes são desprezíveis. Dados: O volume do tambor é 200 dm³;  a parte oca possui o volume de 80 dm³; pressão local 1 atm e a temperatura ambiente 20ºC.

Calcular a densidade do tambor, utilizando uma balança (com graduação em kg), para medir a massa do tambor e aplicando o volume total deste. O tambor possui volume de 200 dm³ (= 200 litros) e sua massa medida é de 120 kg

Logo, a densidade é:

d = m/V
d = 120/200 x 10^-3
d = 600 kg/m³

Então a densidade do tambor é d = 0,6 kg/dm³

Calcular a massa especifica, sabendo-se que o volume da parte oca V = 80 dm³.

O volume da parte não oca (da água, que nos interessa) é: 200 – 80 = 120 dm³ (= volume total do tambor diminuído da parte oca).

ρ =  m/V

ρ = 120/120 x 10^-3

ρ = 1000 kg/m³

Sendo a mesma equação utilizada, massa específica e densidade têm conceitos diferentes.

Massa específica e densidade são ambas a razão entre massa e o volume de um corpo. No entanto, a massa específica é sempre constante e a densidade varia conforme o corpo.

Massa específica

Vamos considerar uma porção de uma determinada substância homogênea (pois todos os pontos dessa substância apresentam as mesmas propriedades) e maciça. Essa porção possui massa e volume, então podemos verificar que a razão entre sua massa e seu volume tem sempre um mesmo valor. A esse valor constante chamamos de massa específica (ρ).

Sendo assim, a massa específica é característica de cada substância e pode ser definida como sendo a razão entre a massa e o volume correspondente. Massa específica é representada pela equação:

Para uma determinada substância, a massa específica é sempre a mesma, então a massa dessa substância é diretamente proporcional ao volume ocupado por ela.

Densidade

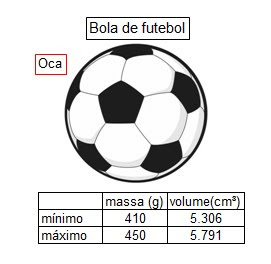
Vamos agora considerar um corpo de massa m e volume V que pode ser heterogêneo ou oco (como mostra a figura abaixo):

Esse corpo (bola de futebol) possui uma massa m e um volume V, que inclui a parte vazia (oca). Dessa forma, podemos definir densidade como:

(A densidade de um corpo é dada pela razão entre a massa e o volume correspondente.)

As unidades dimensionais de densidade e massa específica são as mesmas. Vimos que a massa específica de uma substância é constante, já a densidade varia conforme o corpo. Mesmo sendo a mesma equação utilizada, massa específica e densidade têm conceitos diferentes.

Definimos massa específica como sendo a razão da massa e do volume de uma substância maciça, por exemplo: uma esfera de ferro.

Temos que ficar atentos, pois um sólido oco apresenta densidade menor que a massa específica do material que o constitui.