TRABALHO DE UMA FORÇA QUALQUER

Uma força F variável em módulo, direção e sentido atua num ponto material que descreve uma trajetória curva AB qualquer (Fig-01a). Em intervalos de tempos infinitesimais Δt₁, Δt₂, ... a força F tem intensidades F₁, F₂, ... e seu ponto de aplicação sofre os deslocamentos infinitesimais Δs₁, Δs₂, ... . Os trabalhos infinitesimais de F₁, F₂ ... são:

Nas expressões anteriores, tem-se que:

(é a projeção da força na direção do deslocamento)

Logo,

Portanto,

O trabalho da força F de A até B será a somatória (Σ) dos trabalhos anteriores.

O cálculo direto da soma acima envolve dificuldades matemáticas que serão vistos no curso superior (Cálculo Integral).  No entanto, esse cálculo pode ser efetuado com ajuda gráfica como mostra na figura (Fig-01b) (F_t indica a projeção da força na direção do deslocamento).

O trabalho ΔT=F_t.Δs, realizado durante um pequeno deslocamento Δs, corresponde à área de estreita faixa retangular. O trabalho total realizado pela força de A até B é a soma das áreas dos retângulos semelhantes ao anterior.  Assim, o trabalho total é numericamente igual à área total sombreada na Fig-01b.

O cálculo dessa área “hachurada” (Fig-01b) corresponde ao cálculo da soma Σ(ΔT).

Trabalho

Em física, TRABALHO está associado a forças e não a corpos: diz-se “trabalho de uma força” e nunca “trabalho de um corpo”.

Para iniciar veremos trabalho de uma força constante em dois casos particulares: paralela e não paralela ao deslocamento.

TRABALHO DE UMA FORÇA CONSTANTE (Paralela ao deslocamento)

Seja (Fig-01) uma força constante, paralela e de mesmo sentido que o deslocamento retilíneo AB que o corpo efetua devido à ação do conjunto de forças que nele atuam.  Se d é o módulo do deslocamento e F a intensidade da força, definimos o trabalho T (letra grega “tau”) da força:

Trabalho T da força constante F, paralela e de mesmo sentido que o deslocamento retilíneo AB, é a grandeza escalar:

Se a intensidade da força estiver em “newtons” e a distância em “metros”, a unidade de trabalho será “joule” ( J ).

A força que favorece o deslocamento do corpo é uma força FORÇA MOTORA; seu trabalho é MOTOR e é POSITIVO (Fig-02).

Quando a força se opõe ao deslocamento é uma FORÇA RESISTENTE; seu trabalho será RESISTENTE e é NEGATIVO (Fig-02).

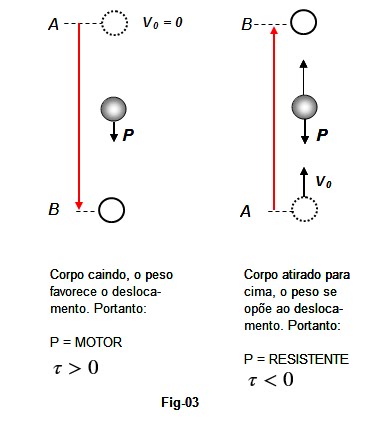
Exemplo (Fig-03):

Se abandonarmos um corpo, seu peso favorece o deslocamento: nesse caso é uma força motora e seu trabalho positivo. Porém, se atirarmos um corpo para cima seu deslocamento será para cima e o peso resistente, porque se opõe ao deslocamento: seu trabalho será resistente e negativo.

(Resumo) Observamos que:

1. Trabalho de uma força;
2. Trabalho num deslocamento (entre 2 pontos);
3. Trabalho é uma grandeza escalar;
4. Trabalho depende do referencial;
5. Trabalho pode ser positivo, ou negativo, conforme a força favoreça, ou se oponha ao deslocamento.

TRABALHO DE UMA FORÇA CONSTANTE (Não paralela ao deslocamento)

Se pegarmos a projeção da força F (Fig-04), na direção do deslocamento, sua projeção (componente da força F) será paralela a ele. Então podemos aplicar a definição anterior. O trabalho da força F será:

É fácil verificar que a projeção de F é igual a F_*cosθ, basta aplicar as propriedades de trigonometria.

Portanto,

Fisicamente é correto, também, projetar o deslocamento na direção da força (Fig-05) e aplicar, novamente, a definição de trabalho, pois, a força e a projeção do deslocamento são paralelas.

OBSERVAÇÕES

Quando a força F é perpendicular ao deslocamento AB, sua projeção (ou a projeção de seu deslocamento) será nula: daí, seu trabalho é nulo. Assim, em um deslocamento horizontal o peso e a reação normal do apoio têm trabalhos nulos (Fig-06).

Analogamente, a força centrípeta tem trabalho nulo, pois é sempre perpendicular ao deslocamento (Fig-06).

FORÇA PESO - UM CASO NOTÁVEL 

Seja AB um deslocamento vertical e “h” o módulo do desnível entre A e B (Fig-07). Como peso P é constante e paralelo ao deslocamento AB:

Se o corpo cai, o peso está a favor do deslocamento (Fig-08a) e o trabalho é motor (positivo). Se o corpo estiver subindo, o peso tem sentido contrário ao deslocamento (Fig-08b) e o trabalho é resistente (negativo).

Se o corpo vai de A até B passando por um ponto C intermediário (Fig-09), projetamos o deslocamento na direção do peso.  Sejam h₁ a projeção vertical de AC e h₂ a projeção vertical de CB.

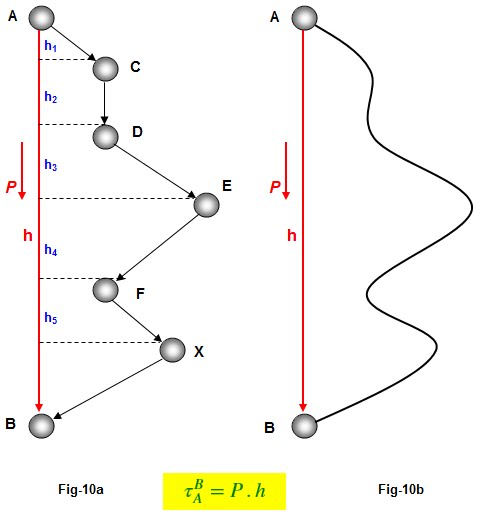
Considere agora (Fig-10a) uma sucessão de segmentos retilíneos AC, CD, DE, ..., XB de A até B. Pelo mesmo raciocínio anterior sejam h₁, h₂, ..., h_n, as projeções verticais desses segmentos.

Se a linha poligonal ACDE...B possuir um conjunto demasiadamente grande de segmentos (Fig-10b) tenderá a uma curva. Porém, o trabalho do peso continua a ser o mesmo. É INDEPENDENTE DA TRAJETÓRIA

TRABALHO DO PESO

A)   Positivo quando o corpo desce;

B)   Negativo quando o corpo sobe;

C)   Nulo em deslocamento horizontal;

D)   Só depende do próprio peso e do desnível entre a posição inicial e final;

E)    Não depende da forma da trajetória.

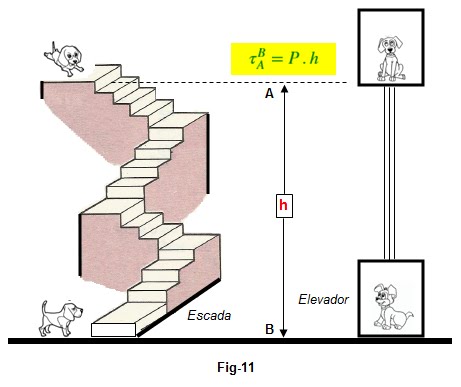
O Trabalho do peso é (P.h) não depende da trajetória.