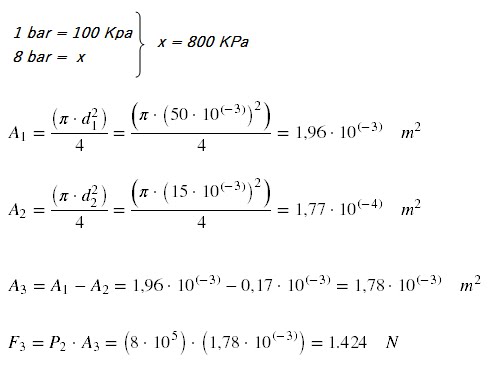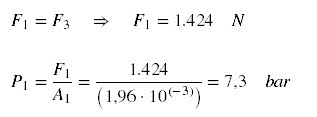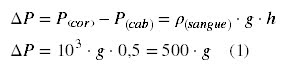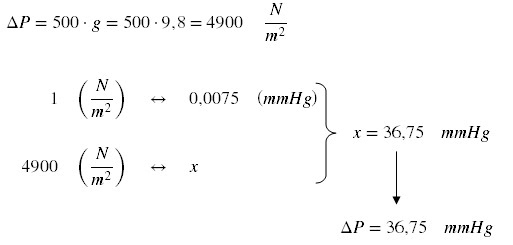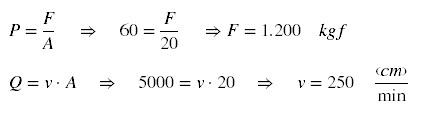Hidráulica-Ex.Resolvidos-2

Ex-01

Um tubo admite água (ρ = 1000 kg/m³) num reservatório com uma vazão de 20 litros/segundo.  No mesmo reservatório é trazido óleo (ρ = 800 kg/m³) por outro tubo com uma vazão de 10 litros/segundo. A mistura homogênea formada é descarregada por um tubo cuja seção tem uma área de 30 cm². Determine a massa específica da mistura no tubo de descarga e a velocidade da mesma.

Solução

Pela equação da conservação de massa em um escoamento em regime, tem-se:

Sabemos que:

Reescrevendo a determinação da vazão em função da velocidade média do escoamento e da área da seção formada pelo fluido, tem-se:

Ex-02

Considere o esquema de um cilindro de dupla ação:

A) Sabendo que a pressão P2 é de 8 bar, calcular a força aplicada no cilindro para ele retornar.

B) Qual a pressão (P1) em bar para manter o cilindro parado?

Solução

A) Terá que aplicar uma força maior que 1.424 N.

B) 

Ex-03

Em um prédio de apartamentos residenciais será instalado um sistema de bombeamento de água para elevar o volume de 18.000 litros (L) de água, em um tempo de 45 min.

O desnível entre o fundo do reservatório subterrâneo e o ponto de descarga no reservatório superior é de 36 m.

Considere:

g = 9,8 m/s² (aceleração da gravidade local)

μ_b = 0,8 (rendimento da bomba)

ρ_H2O= 1 Kg/l

• Qual a potência da bomba a ser instalada?

Solução

1) Vazão do fluxo (Q)

2) Potência (P)

Portanto,

Como comercialmente o valor é dado em CV:

Ex-04

Em um prédio de apartamentos residenciais será instalado um sistema de bombeamento de água para elevar o volume de 30 m³ de água em um tempo de 1 hora. Sabendo-se que o reservatório inferior está 10 m abaixo do nível da rua e o reservatório superior encontra-se no topo do prédio de 20 andares, sendo o pé direito de cada andar de 2,80 m. Dimensionar a bomba e fazer previsão de consumo de energia.

Solução

Consumo:

Ex-05

Dimensione o diâmetro (d) da tubulação de um sistema de bombeamento de água cuja bomba possui vazão Q=60 l/min. O tempo de trabalho diário da bomba é t=3 h (por dia).

Solução

Vazão da bomba (m³/s):

Diâmetro da tubulação (d):

Sendo Q = vazão do fluido (m³/s) e x = proporção de horas diárias de funcionamento da bomba.

Ex-06

Dada uma bomba para bombeamento de óleo cuja vazão Q = 100 l/s e o tempo de trabalho dessa bomba é de 8h/dia. Dimensione o diâmetro (d) da tubulação.

Solução

Vazão da bomba (m³/s):

Diâmetro da tubulação:

Ex-07 (COVEST-PE)

Se o fluxo sanguíneo não fosse ajustado pela expansão de artérias, para uma pessoa em pé a diferença de pressão arterial entre o coração e a cabeça seria de natureza puramente hidrostática. Nesse caso, para uma pessoa em que a distância entre a cabeça e o coração vale 50 cm, qual o valor em mmHg dessa diferença de pressão? (Considere a densidade do sangue igual a 10³ kg/m³ e a densidade do mercúrio igual a 13,6x10³ kg/m³).

Solução:

Aplicando o Princípio de Stevin:

Para calcular a pressão em coluna de mercúrio, basta calcular a pressão da coluna de mercúrio equivalente a ∆P.

Igualando as equações (1) e (2), tem-se:

Portanto, a diferença pressão (em mmHg) é ∆P = 36,76 mmHg

Outra maneira de resolver:

Caso a questão seja de múltipla alternativa, existe outro caminho talvez mais rápido, porém, tem que saber e adotar os seguintes dados: g = 9,8 m/s² (aceleração da gravidade) e 1 (N/m², PA) = 0,0075 (mmHg).

Equação (1): 

Ex-08 (UnB-DF)

Temos dois tubos cilíndricos, A e B de diâmetros D e D/4, respectivamente. Os cilindros formam um sistema de macaco hidráulico e os êmbolos são móveis. Considerando o sistema em equilíbrio e desprezando o peso dos êmbolos, ache a razão entre as intensidades das forças F_A/F_B. 

Solução:

Pelo princípio de Pascal, tem-se:

 Ex-09 (FUVEST-SP)

As esferas maciças A e B, que têm o mesmo volume e foram coladas, estão em equilíbrio, imersas na água. Quando a cola que as une se desfaz, a esfera A sobe e passa a flutuar, com metade de seu volume fora da água (densidade da água: 1 g/cm³).

A) Qual é a densidade da esfera A?

B) Qual é a densidade da esfera B?

Solução:

A) 

Esfera A em situação de flutuação na superfície da água.

Seja V o volume da esfera A.

B)

Ex-10

Um cilindro hidráulico de dupla ação contém, as seguintes características:

Área de avanço A₁ = 20 cm²

Área de retorno A₂ = 10 cm²

Curso do atuador S_at = 200 mm.

Calcular a força e velocidade que o atuador exerce no avanço e no retorno com uma pressão de trabalho (p) de 60 kgf/cm² e vazão (Q) de 5000 cm³/min.

Solução

No avanço

No retorno

Relembrando Hidrostática

Já vimos em alguma parte do passado recente que a Hidrostática é parte da Física que estuda os fluídos (líquido e gás) em repouso (que não estejam em escoamento (=movimento)).

1. Massa Específica

É a relação entre massa e volume ocupado por esta massa. E essa relação é definida para corpos homogêneos.

Sendo:

ρ = massa específica

m = massa de corpo homogêneo

V = volume ocupado pela massa

2. Densidade

A relação, também, é entre a massa e volume, porém, corpos não homogêneos.

Sendo:

d = densidade

m’ = massa de corpo não homogêneo

V’ = volume ocupado por este corpo

3. Pressão

A pressão é definida como a aplicação de uma determinada força distribuída sobre uma área.

Nota: A unidade de medida da pressão é Newton por metro quadrado (N/m²).  No caso de fluídos o Newton por metro quadrado é, também, denominado de pascal (Pa).

4. Princípio de Stevin

O princípio de Stevin nos permite calcular a pressão em um líquido em repouso, estando com sua superfície livre em contato com a atmosfera.

Sendo:

P_A = pressão num certo ponto A do líquido

P_atm = pressão atmosférica

ρ = massa específica do liquido

g = aceleração da gravidade

h = profundidade do ponto A

(h + h’) = profundidade do ponto B

5. Princípio de Pascal

Um acréscimo de pressão exercido em qualquer ponto de um fluido é transmitido para todo o fluido.

Como a pressão é igual em todos os pontos do fluído, podemos escrever a seguinte equação:

Portanto, se a área A₁ é 4 vezes maior que a área A₂, temos um amplificador de força F₁ = 4_*F₂

6. Princípio de Arquimedes

Todo corpo mergulhado em um fluido (liquido, ou gás) sofre, devido a este (ao fluido), uma ação de força vertical para cima (Empuxo), cuja intensidade é igual ao peso do fluido deslocado pelo corpo.

AS EQUAÇÕES:

Seja V_F o volume do fluido deslocado pelo corpo. Então a massa do fluido deslocado (m_F) é calculada pela seguinte relação:

Sendo:

m_F = massa do fluido deslocado (Kg)

ρ_F = densidade do fluido (Kg/m³)

V_F = Volume do fluido deslocado (m³)

A intensidade do empuxo é igual à do peso dessa massa deslocada:

Sendo,

g = aceleração da gravidade (m/s²)

As equações a seguir valem para corpos totalmente imersos. Portanto, o volume do fluido deslocado é igual ao próprio volume do corpo.

Sendo:

P = peso do corpo (N)

ρ_C = densidade do corpo (Kg/m³)

V_C = Volume do corpo (m³)

g = aceleração da gravidade (m/s²)

E = empuxo (N)

ρ_F = densidade do fluido (Kg/m³)

V_F = Volume do fluido deslocado (m³)

Se o empuxo for maior que a força peso, a tendência do corpo é de subir com aceleração. Caso peso seja maior que o empuxo, a tendência é de o corpo descer com aceleração. Tanto no primeiro caso, ou no segundo a força resultante é diferente de zero (vale a 2ª Lei de Newton, Princípio Fundamental da Dinâmica). Quando o empuxo for igual à força peso, a tendência do corpo é permanecer parado.

7. Curiosidade:

O submarino funciona de acordo com o Princípio de Arquimedes.

Um submarino ou qualquer tipo de navio pode flutuar porque o peso da água deslocada é igual ao peso da embarcação. Esse deslocamento de água cria uma força que puxa para cima, chamada força de flutuação (Empuxo), e age em oposição à gravidade que puxa a embarcação para baixo. Diferente do navio, o submarino pode controlar a sua flutuação, podendo assim submergir e emergir conforme a necessidade.

Para controlar a flutuação, o submarino possui tanques de lastro e auxiliares, ou tanques de balanceamento, que podem, alternadamente, serem enchidos com água ou ar.

Salvo em situações de emergência, um submarino ao tentar submergir, (ou emergir) não inunda, (ou não solta) subitamente toda a água em seus tanques de lastro. Essa ação súbita provocaria uma descida, (ou subida) acelerada difícil de ser controlada.   A inundação, ou liberação de água dos tanques de lastro é feita de forma controlada, de modo a manter a força de empuxo igual à força peso e desta maneira conseguir afundar ou subir gradualmente com velocidade constante. O controle de descida, ou subida gradual é feito pela hélice de propulsão em conjunto com as aletas controladoras de movimento vertical (hidroplanos) que se localizam na popa (parte de trás).

Quando o submarino está na superfície, os tanques de lastro estão cheios de ar, portanto, a densidade do submarino é menor que a da água circundante. Para mergulhar o submarino enche os seus tanques de lastro de água até que a densidade seja maior do que da água. Como conseqüência o submarino entra na condição de flutuação negativa e começa a afundar. Os hidroplanos juntamente com a hélice de propulsão, na popa, são utilizados para controlar o ângulo de mergulho.  (Os hidroplanos são posicionados de forma a permitir que a água se mova debaixo da popa, fazendo-a mover-se para cima, como resultado, o submarino desloca-se para baixo).

Para que o submarino mantenha o nivelamento a certa profundidade, mantém o equilíbrio entre água e ar nos seus tanques de lastro, para que a densidade seja igual à da água circundante (condição de flutuação neutra).  

Em flutuação neutra os hidroplanos são ajustados de forma que o submarino se mantenha a profundidade e movimentados para executar pequenas correções no nível. A água é injetada nos tanques auxiliares de popa e proa para manter o submarino nivelado na horizontal. O submarino pode de movimentar na água usando as hélices de propulsão e leme da cauda para virar a estibordo (direita), a bombordo (esquerda); e os hidroplanos para controlar o ângulo de proa a popa.

Para emergir o ar comprimido flui dos tanques de ar para os tanques de lastro e a água é forçada a sair, até que atinja a condição de flutuação positiva, isto é, a densidade do submarino seja inferior que a da água em sua volta. Os hidroplanos são posicionados de forma que a água se mova sobre a popa, forçando a parte traseira do submarino para baixo, assim o submarino é apontado para cima.

Diferença entre Densidade e Massa específica

Geralmente, usa-se "densidade" para representar a razão entre a massa e o volume de objetos sólidos (ocos ou maciços).  E "massa específica" para fluidos (líquidos e gases) e substâncias.

Um exemplo para ilustrar:

Para ficar mais fácil entender imagine um tambor com uma parte oca dentro, a parte oca está vazia, e o resto do cilindro preenchido de água. 

Supondo que o tambor é ideal, isto é, sua massa e espessura das paredes são desprezíveis. Dados: O volume do tambor é 200 dm³;  a parte oca possui o volume de 80 dm³; pressão local 1 atm e a temperatura ambiente 20ºC.

Calcular a densidade do tambor, utilizando uma balança (com graduação em kg), para medir a massa do tambor e aplicando o volume total deste. O tambor possui volume de 200 dm³ (= 200 litros) e sua massa medida é de 120 kg

Logo, a densidade é:

d = m/V
d = 120/200 x 10^-3
d = 600 kg/m³

Então a densidade do tambor é d = 0,6 kg/dm³

Calcular a massa especifica, sabendo-se que o volume da parte oca V = 80 dm³.

O volume da parte não oca (da água, que nos interessa) é: 200 – 80 = 120 dm³ (= volume total do tambor diminuído da parte oca).

ρ =  m/V

ρ = 120/120 x 10^-3

ρ = 1000 kg/m³

Sendo a mesma equação utilizada, massa específica e densidade têm conceitos diferentes.

Massa específica e densidade são ambas a razão entre massa e o volume de um corpo. No entanto, a massa específica é sempre constante e a densidade varia conforme o corpo.

Massa específica

Vamos considerar uma porção de uma determinada substância homogênea (pois todos os pontos dessa substância apresentam as mesmas propriedades) e maciça. Essa porção possui massa e volume, então podemos verificar que a razão entre sua massa e seu volume tem sempre um mesmo valor. A esse valor constante chamamos de massa específica (ρ).

Sendo assim, a massa específica é característica de cada substância e pode ser definida como sendo a razão entre a massa e o volume correspondente. Massa específica é representada pela equação:

Para uma determinada substância, a massa específica é sempre a mesma, então a massa dessa substância é diretamente proporcional ao volume ocupado por ela.

Densidade

Vamos agora considerar um corpo de massa m e volume V que pode ser heterogêneo ou oco (como mostra a figura abaixo):

Esse corpo (bola de futebol) possui uma massa m e um volume V, que inclui a parte vazia (oca). Dessa forma, podemos definir densidade como:

(A densidade de um corpo é dada pela razão entre a massa e o volume correspondente.)

As unidades dimensionais de densidade e massa específica são as mesmas. Vimos que a massa específica de uma substância é constante, já a densidade varia conforme o corpo. Mesmo sendo a mesma equação utilizada, massa específica e densidade têm conceitos diferentes.

Definimos massa específica como sendo a razão da massa e do volume de uma substância maciça, por exemplo: uma esfera de ferro.

Temos que ficar atentos, pois um sólido oco apresenta densidade menor que a massa específica do material que o constitui.